How Do You Know When to Use Single Silit Over Circular Aperture

Diffraction

29 Circular Apertures and Resolution

Learning Objectives

By the end of this section, you will be able to:

Describe the diffraction limit on resolution
Draw the diffraction limit on axle propagation

Calorie-free diffracts equally it moves through infinite, angle around obstacles, interfering constructively and destructively. This can be used as a spectroscopic tool—a diffraction grating disperses light co-ordinate to wavelength, for example, and is used to produce spectra—only diffraction also limits the detail we tin can obtain in images.

(Figure)(a) shows the effect of passing calorie-free through a small circular discontinuity. Instead of a bright spot with sharp edges, nosotros obtain a spot with a fuzzy edge surrounded by circles of light. This blueprint is acquired by diffraction, similar to that produced past a single slit. Lite from different parts of the circular aperture interferes constructively and destructively. The result is most noticeable when the aperture is small, but the effect is there for big apertures as well.

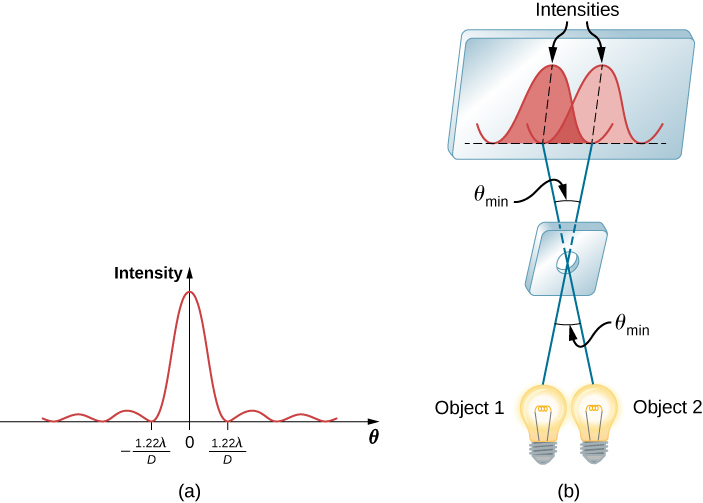
(a) Monochromatic light passed through a small round discontinuity produces this diffraction pattern. (b) Two point-low-cal sources that are close to one another produce overlapping images because of diffraction. (c) If the sources are closer together, they cannot exist distinguished or resolved.

Figure a shows a bright white circle on a black background. Its edge is diffused. Figures b and c show two white circles overlapping. The circles in figure c are closer to each other than those in figure b.

How does diffraction affect the detail that can be observed when lite passes through an aperture? (Figure)(b) shows the diffraction pattern produced past two indicate-lite sources that are shut to one another. The pattern is similar to that for a single point source, and it is withal possible to tell that at that place are ii light sources rather than one. If they are closer together, as in (Figure)(c), nosotros cannot distinguish them, thus limiting the particular or resolution we can obtain. This limit is an inescapable consequence of the wave nature of calorie-free.

Diffraction limits the resolution in many situations. The vigil of our vision is limited considering light passes through the pupil, which is the circular aperture of the eye. Exist enlightened that the diffraction-like spreading of calorie-free is due to the limited bore of a light beam, not the interaction with an aperture. Thus, light passing through a lens with a diameter D shows this effect and spreads, blurring the image, just as lite passing through an aperture of bore D does. Thus, diffraction limits the resolution of any system having a lens or mirror. Telescopes are also limited past diffraction, because of the finite diameter D of the principal mirror.

Just what is the limit? To reply that question, consider the diffraction pattern for a circular aperture, which has a central maximum that is wider and brighter than the maxima surrounding it (similar to a slit) ((Figure)(a)). It can be shown that, for a circular aperture of diameter D, the first minimum in the diffraction pattern occurs at $\theta =1.22\text{λ}\text{/}D$ (providing the aperture is large compared with the wavelength of lite, which is the case for most optical instruments). The accepted criterion for determining the diffraction limit to resolution based on this angle is known every bit the Rayleigh criterion, which was developed past Lord Rayleigh in the nineteenth century.

Rayleigh Benchmark

The diffraction limit to resolution states that two images are only resolvable when the center of the diffraction pattern of i is direct over the first minimum of the diffraction blueprint of the other ((Figure)(b)).

The first minimum is at an angle of $\theta =1.22\text{λ}\text{/}D$ , then that two point objects are but resolvable if they are separated by the angle

$\theta =1.22\frac{\text{λ}}{D}$

where $\text{λ}$ is the wavelength of light (or other electromagnetic radiations) and D is the diameter of the aperture, lens, mirror, etc., with which the two objects are observed. In this expression, $\theta$ has units of radians. This bending is also commonly known equally the diffraction limit.

(a) Graph of intensity of the diffraction pattern for a round aperture. Annotation that, similar to a unmarried slit, the central maximum is wider and brighter than those to the sides. (b) 2 point objects produce overlapping diffraction patterns. Shown here is the Rayleigh criterion for being just resolvable. The central maximum of one blueprint lies on the outset minimum of the other.

All attempts to observe the size and shape of objects are express past the wavelength of the probe. Even the small-scale wavelength of lite prohibits verbal precision. When extremely small-scale wavelength probes are used, equally with an electron microscope, the organization is disturbed, notwithstanding limiting our knowledge. Heisenberg's uncertainty principle asserts that this limit is cardinal and inescapable, every bit we shall run into in the chapter on quantum mechanics.

Calculating Diffraction Limits of the Hubble Space Telescope The main mirror of the orbiting Hubble Space Telescope has a diameter of 2.40 m. Being in orbit, this telescope avoids the degrading effects of atmospheric distortion on its resolution. (a) What is the angle between two simply-resolvable betoken calorie-free sources (perhaps 2 stars)? Assume an average light wavelength of 550 nm. (b) If these two stars are at a distance of two meg calorie-free-years, which is the altitude of the Andromeda Galaxy, how shut together can they exist and still be resolved? (A lite-twelvemonth, or ly, is the distance light travels in i year.)

Strategy The Rayleigh benchmark stated in (Figure), $\theta =1.22\text{λ}\text{/}D$ , gives the smallest possible angle $\theta$ between signal sources, or the best obtainable resolution. One time this angle is known, we can calculate the distance betwixt the stars, since we are given how far away they are.

Solution

The Rayleigh benchmark for the minimum resolvable angle is

$\theta =1.22\frac{\text{λ}}{D}.$

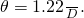
Entering known values gives

$\theta =1.22\frac{550\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{−}9}\phantom{\rule{0.2em}{0ex}}\text{m}}{2.40\phantom{\rule{0.2em}{0ex}}\text{m}}=2.80\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{−}7}\phantom{\rule{0.2em}{0ex}}\text{rad}.$
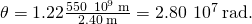
The distance s between ii objects a distance r away and separated by an bending 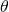$\theta$ is $s=r\theta .$
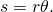
Substituting known values gives

$s=\left(2.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{6}\phantom{\rule{0.2em}{0ex}}\text{ly}\right)\left(2.80\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{−}7}\phantom{\rule{0.2em}{0ex}}\text{rad}\right)=0.56\phantom{\rule{0.2em}{0ex}}\text{ly}.$

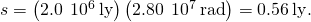
Significance The angle found in function (a) is extraordinarily small (less than 1/50,000 of a caste), because the chief mirror is and then large compared with the wavelength of light. Equally noticed, diffraction effects are most noticeable when light interacts with objects having sizes on the order of the wavelength of light. However, the issue is still at that place, and in that location is a diffraction limit to what is observable. The actual resolution of the Hubble Telescope is not quite as expert equally that found here. Every bit with all instruments, there are other effects, such as nonuniformities in mirrors or aberrations in lenses that further limit resolution. Nonetheless, (Figure) gives an indication of the extent of the detail observable with the Hubble considering of its size and quality, and especially because it is above Globe'southward atmosphere.

These two photographs of the M82 Galaxy give an idea of the observable item using (a) a ground-based telescope and (b) the Hubble Space Telescope. (credit a: modification of work past "Ricnun"/Wikimedia Commons; credit b: modification of work by NASA, ESA, and The Hubble Heritage Team (STScI/AURA))

Figures a and b show telescopic images of a galaxy.

The answer in part (b) indicates that two stars separated by about half a lite-year tin can exist resolved. The average altitude between stars in a galaxy is on the order of five lite-years in the outer parts and about one lite-year near the galactic center. Therefore, the Hubble can resolve most of the individual stars in Andromeda Galaxy, even though it lies at such a huge distance that its light takes 2 one thousand thousand years to reach us. (Effigy) shows another mirror used to observe radio waves from outer space.

A 305-one thousand-diameter paraboloid at Arecibo in Puerto Rico is lined with reflective cloth, making it into a radio telescope. It is the largest curved focusing dish in the globe. Although D for Arecibo is much larger than for the Hubble Telescope, it detects radiation of a much longer wavelength and its diffraction limit is significantly poorer than Hubble'due south. The Arecibo telescope is still very useful, considering of import information is carried by radio waves that is not carried by visible lite. (credit: Jeff Hitchcock)

Photograph shows a large parabolic surface.

Check Your Understanding What is the angular resolution of the Arecibo telescope shown in (Figure) when operated at 21-cm wavelength? How does it compare to the resolution of the Hubble Telescope?

$8.4\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-4}\phantom{\rule{0.2em}{0ex}}\text{rad}$ , 3000 times broader than the Hubble Telescope

Diffraction is not only a problem for optical instruments merely also for the electromagnetic radiation itself. Any beam of light having a finite diameter D and a wavelength $\text{λ}$ exhibits diffraction spreading. The axle spreads out with an angle $\theta$ given past (Figure), $\theta =1.22\lambda \text{/}D$ . Take, for example, a laser axle made of rays every bit parallel every bit possible (angles between rays every bit close to $\theta =0\text{°}$ as possible) instead spreads out at an angle $\theta =1.22\text{λ}\text{/}D$ , where D is the diameter of the beam and $\text{λ}$ is its wavelength. This spreading is impossible to discover for a flashlight considering its beam is non very parallel to start with. However, for long-altitude transmission of laser beams or microwave signals, diffraction spreading tin can be meaning ((Effigy)). To avoid this, we can increase D. This is washed for light amplification by stimulated emission of radiation light sent to the moon to measure its distance from Globe. The laser beam is expanded through a telescope to make D much larger and $\theta$ smaller.

The beam produced by this microwave transmission antenna spreads out at a minimum angle $\theta =1.22\text{λ}\text{/}D$ due to diffraction. It is impossible to produce a near-parallel beam because the beam has a express diameter.

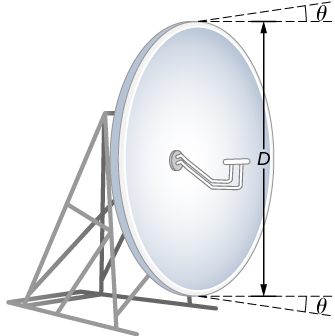
Figure shows a dish antenna with diameter D. Lines emerging from two edges of the dish form an angle theta with the horizontal.

In most biology laboratories, resolution is an issue when the use of the microscope is introduced. The smaller the distance ten by which two objects can be separated and notwithstanding be seen as distinct, the greater the resolution. The resolving ability of a lens is defined as that distance x. An expression for resolving power is obtained from the Rayleigh criterion. (Figure)(a) shows two bespeak objects separated by a distance x. Co-ordinate to the Rayleigh benchmark, resolution is possible when the minimum angular separation is

$\theta =1.22\frac{\text{λ}}{D}=\frac{x}{d},$

where d is the distance between the specimen and the objective lens, and we have used the small angle approximation (i.e., we have causeless that x is much smaller than d), and so that $\text{tan}\phantom{\rule{0.2em}{0ex}}\theta \approx \phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\theta \approx \theta .$ Therefore, the resolving power is

$x=1.22\frac{\text{λ}d}{D}.$

Another way to look at this is by the concept of numerical aperture (NA), which is a mensurate of the maximum acceptance bending at which a lens will have lite and still contain it inside the lens. (Effigy)(b) shows a lens and an object at point P. The NA hither is a measure of the ability of the lens to assemble calorie-free and resolve fine detail. The angle subtended by the lens at its focus is defined to exist $\theta =2\alpha$ . From the effigy and again using the small-scale angle approximation, we tin write

$\text{sin}\phantom{\rule{0.2em}{0ex}}\alpha =\frac{D\text{/}2}{d}=\frac{D}{2d}.$

The NA for a lens is $NA=n\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\alpha$ , where n is the index of refraction of the medium betwixt the objective lens and the object at indicate P. From this definition for NA, we can see that

$x=1.22\frac{\text{λ}d}{D}=1.22\frac{\text{λ}}{2\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\alpha }=0.61\frac{\text{λ}n}{NA}.$

In a microscope, NA is important because information technology relates to the resolving power of a lens. A lens with a big NA is able to resolve effectively details. Lenses with larger NA are also able to collect more light and and so give a brighter image. Another way to describe this state of affairs is that the larger the NA, the larger the cone of light that can exist brought into the lens, and so more of the diffraction modes are collected. Thus the microscope has more information to class a clear image, and its resolving power is higher.

(a) 2 points separated by a distance ten and positioned a altitude d abroad from the objective. (b) Terms and symbols used in discussion of resolving power for a lens and an object at point P (credit a: modification of work by "Infopro"/Wikimedia Commons).

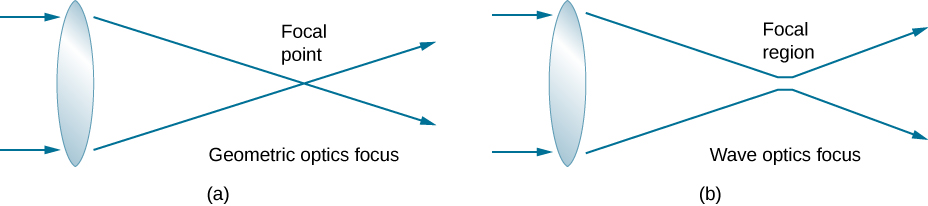
Ane of the consequences of diffraction is that the focal point of a beam has a finite width and intensity distribution. Imagine focusing when only considering geometric optics, as in (Effigy)(a). The focal signal is regarded every bit an infinitely small point with a huge intensity and the chapters to incinerate nigh samples, irrespective of the NA of the objective lens—an unphysical oversimplification. For wave optics, due to diffraction, we take into account the phenomenon in which the focal point spreads to go a focal spot ((Figure)(b)) with the size of the spot decreasing with increasing NA. Consequently, the intensity in the focal spot increases with increasing NA. The college the NA, the greater the chances of photodegrading the specimen. However, the spot never becomes a true signal.

(a) In geometric optics, the focus is modelled as a point, only information technology is not physically possible to produce such a point because information technology implies infinite intensity. (b) In wave optics, the focus is an extended region.

Figures a and b show two rays entering a lens from the left. In figure a, the rays emerge on the right and intersect each other at the focal point. This is labeled geometric optics focus. In figure b, the rays emerge, move towards each other, but do not intersect. The region where they come closest is labeled focal region. The rays diverge from here. This is labeled wave optics focus.

In a different type of microscope, molecules inside a specimen are made to emit light through a mechanism called fluorescence. By controlling the molecules emitting light, it has get possible to construct images with resolution much finer than the Rayleigh criterion, thus circumventing the diffraction limit. The development of super-resolved fluorescence microscopy led to the 2022 Nobel Prize in Chemistry.

In this Optical Resolution Model, two diffraction patterns for lite through ii circular apertures are shown side by side in this simulation by Fu-Kwun Hwang. Lookout man the patterns merge every bit you decrease the aperture diameters.

Summary

Diffraction limits resolution.
The Rayleigh criterion states that two images are just resolvable when the center of the diffraction design of one is straight over the first minimum of the diffraction pattern of the other.

Conceptual Questions

Is higher resolution obtained in a microscope with red or blue light? Explain your answer.

blue; The shorter wavelength of blue light results in a smaller angle for diffraction limit.

The resolving ability of refracting telescope increases with the size of its objective lens. What other advantage is gained with a larger lens?

The distance between atoms in a molecule is about ${10}^{-8}\phantom{\rule{0.2em}{0ex}}\text{cm}$ . Can visible lite exist used to "encounter" molecules?

No, these distances are three orders of magnitude smaller than the wavelength of visible light, so visible lite makes a poor probe for atoms.

A beam of light always spreads out. Why can a beam not exist created with parallel rays to prevent spreading? Why can lenses, mirrors, or apertures non be used to right the spreading?

Issues

The 305-m-diameter Arecibo radio telescope pictured in (Figure) detects radio waves with a 4.00-cm boilerplate wavelength. (a) What is the angle between two simply-resolvable point sources for this telescope? (b) How close together could these signal sources be at the 2 million lite-yr distance of the Andromeda Galaxy?

Assuming the angular resolution found for the Hubble Telescope in (Figure), what is the smallest detail that could be observed on the moon?

107 m

Diffraction spreading for a flashlight is insignificant compared with other limitations in its optics, such every bit spherical aberrations in its mirror. To testify this, summate the minimum angular spreading of a flashlight beam that is originally 5.00 cm in diameter with an boilerplate wavelength of 600 nm.

(a) What is the minimum angular spread of a 633-nm wavelength He-Ne laser axle that is originally 1.00 mm in diameter? (b) If this laser is aimed at a mountain cliff 15.0 km abroad, how large will the illuminated spot be? (c) How large a spot would exist illuminated on the moon, neglecting atmospheric effects? (This might be done to hit a corner reflector to measure the round-trip time and, hence, distance.)

a. $7.72\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-4}\phantom{\rule{0.2em}{0ex}}\text{rad;}$ b. 23.2 thousand; c. 590 km

A telescope tin can be used to overstate the diameter of a laser axle and limit diffraction spreading. The light amplification by stimulated emission of radiation axle is sent through the telescope in opposite the normal direction and can then be projected onto a satellite or the moon. (a) If this is done with the Mount Wilson telescope, producing a ii.54-thou-diameter beam of 633-nm light, what is the minimum angular spread of the beam? (b) Neglecting atmospheric effects, what is the size of the spot this beam would brand on the moon, assuming a lunar distance of $3.84\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{8}\phantom{\rule{0.2em}{0ex}}\text{m}$ ?

The limit to the middle'due south acuity is actually related to diffraction by the pupil. (a) What is the bending between two just-resolvable points of light for a 3.00-mm-diameter educatee, assuming an average wavelength of 550 nm? (b) Take your result to exist the practical limit for the eye. What is the greatest possible distance a machine tin can be from you if you can resolve its 2 headlights, given they are 1.30 one thousand apart? (c) What is the altitude between two merely-resolvable points held at an arm's length (0.800 m) from your eye? (d) How does your answer to (c) compare to details you normally notice in everyday circumstances?

a. $2.24\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-4}\phantom{\rule{0.2em}{0ex}}\text{rad};$ b. 5.81 km; c. 0.179 mm; d. tin can resolve details 0.ii mm apart at arm's length

What is the minimum diameter mirror on a telescope that would permit you to see details as pocket-sized equally 5.00 km on the moon some 384,000 km away? Assume an average wavelength of 550 nm for the light received.

Find the radius of a star's image on the retina of an heart if its pupil is open to 0.65 cm and the distance from the pupil to the retina is 2.viii cm. Assume $\text{λ}=550\phantom{\rule{0.2em}{0ex}}\text{nm}$ .

$2.9\phantom{\rule{0.2em}{0ex}}\mu \text{m}$

(a) The dwarf planet Pluto and its moon, Charon, are separated by 19,600 km. Neglecting atmospheric effects, should the 5.08-grand-diameter Palomar Mountain telescope be able to resolve these bodies when they are $4.50\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{9}\phantom{\rule{0.2em}{0ex}}\text{km}$ from Earth? Presume an average wavelength of 550 nm. (b) In authenticity, it is only barely possible to discern that Pluto and Charon are separate bodies using a ground-based telescope. What are the reasons for this?

A spy satellite orbits Earth at a height of 180 km. What is the minimum diameter of the objective lens in a telescope that must be used to resolve columns of troops marching 2.0 m apart? Assume $\text{λ}=550\phantom{\rule{0.2em}{0ex}}\text{nm}.$

6.0 cm

What is the minimum athwart separation of ii stars that are just-resolvable past the 8.1-g Gemini South telescope, if atmospheric effects do not limit resolution? Use 550 nm for the wavelength of the lite from the stars.

The headlights of a auto are 1.3 one thousand autonomously. What is the maximum distance at which the eye can resolve these two headlights? Take the pupil diameter to exist 0.xl cm.

7.71 km

When dots are placed on a folio from a laser printer, they must be shut plenty and then that you do not see the individual dots of ink. To practise this, the separation of the dots must be less than Raleigh's benchmark. Take the student of the eye to exist 3.0 mm and the distance from the newspaper to the eye of 35 cm; detect the minimum separation of ii dots such that they cannot exist resolved. How many dots per inch (dpi) does this stand for to?

Suppose you are looking down at a highway from a jetliner flying at an altitude of 6.0 km. How far apart must two cars be if you are able to distinguish them? Presume that $\text{λ}=550\phantom{\rule{0.2em}{0ex}}\text{nm}$ and that the diameter of your pupils is 4.0 mm.

1.0 g

Can an astronaut orbiting Earth in a satellite at a distance of 180 km from the surface distinguish ii skyscrapers that are twenty chiliad apart? Presume that the pupils of the astronaut'southward eyes have a diameter of 5.0 mm and that most of the light is centered around 500 nm.

The characters of a stadium scoreboard are formed with closely spaced lightbulbs that radiate primarily yellow light. (Use $\text{λ}=600\phantom{\rule{0.2em}{0ex}}\text{nm}.$ ) How closely must the bulbs exist spaced so that an observer lxxx thousand away sees a display of continuous lines rather than the individual bulbs? Assume that the educatee of the observer's heart has a diameter of five.0 mm.

1.two cm or closer

If a microscope tin can accept light from objects at angles every bit large as $\alpha =70\text{°}$ , what is the smallest structure that can exist resolved when illuminated with light of wavelength 500 nm and (a) the specimen is in air? (b) When the specimen is immersed in oil, with index of refraction of 1.52?

A photographic camera uses a lens with aperture 2.0 cm. What is the angular resolution of a photograph taken at 700 nm wavelength? Can it resolve the millimeter markings of a ruler placed 35 m away?

Glossary

diffraction limit: cardinal limit to resolution due to diffraction

Rayleigh criterion: two images are but-resolvable when the center of the diffraction pattern of one is directly over the showtime minimum of the diffraction pattern of the other

resolution: ability, or limit thereof, to distinguish small details in images

putmansureence.blogspot.com

Source: https://opentextbc.ca/universityphysicsv3openstax/chapter/circular-apertures-and-resolution/

How Do You Know When to Use Single Silit Over Circular Aperture

29 Circular Apertures and Resolution

Learning Objectives

Summary

Conceptual Questions

Issues

Glossary

0 Response to "How Do You Know When to Use Single Silit Over Circular Aperture"

ارسال یک نظر

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel